Paper review: NN-sort: Neural Network based Data Distribution-aware Sorting
Date: 2021-09-03
Tags: sorting, neural networks
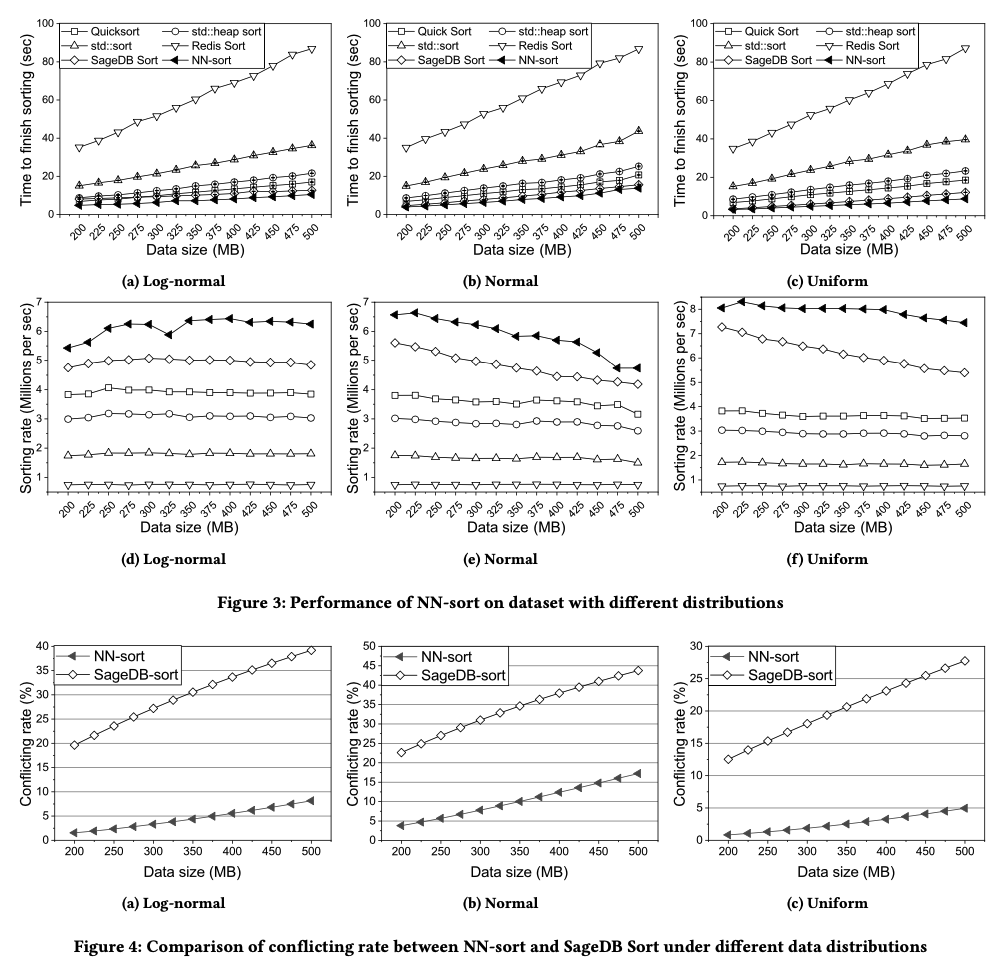
The authors propose a new sorting algorithm called "NN-sort", which leverages the neural network model to learn the data distribution and afterward uses it to map disordered data elements into ordered ones. The complexity of the algorithm is O(N log N) in theory, it can run in near-linear time in most of the cases observed.
NN-SORT Design
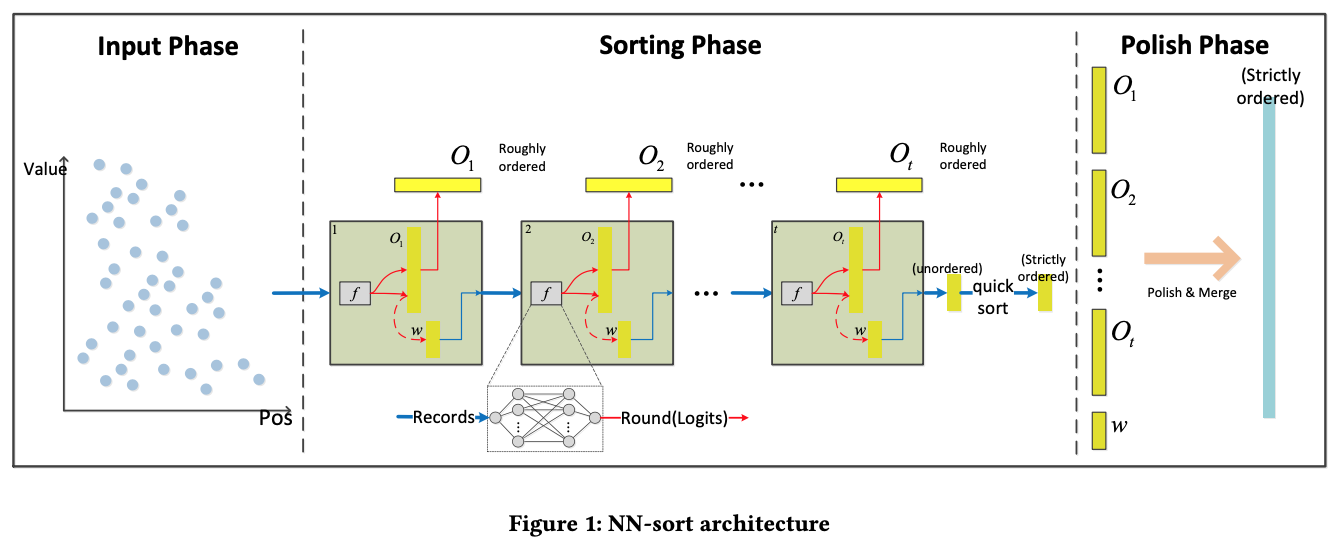
Sorting is performed in multiple rounds: on each round, the model puts the input data into roughly sorted order. If conflicts occur, all the non-conflicts data elements are organized in an array that is roughly ordered, while conflicts data will be put in a conflicting array, which is used as an input of the next iteration. Such iterations continue until the size of the conflicting array is smaller than a threshold. Then, the conflicting array is sorted by classic sorting algorithms, like Quick Sort. In the end, all the roughly ordered arrays and strictly sorted conflicting arrays are merged.
NN-model for NN-SORT
The neural network is composed of 3 hidden layers. The first layer has 32 neurons, while the second layer has 8, the third layer has 4 neurons. Such simple models can be efficiently trained using SGD and they are not so susceptible to overfitting.
In order to avoid the impact of outliers, the model is trained using Huber loss:
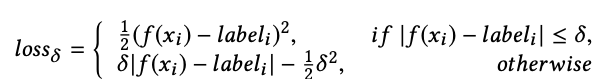
Model Analysis
Best Case
If n > 1, it needs θn operations to sort all the data elements and one pass n operations) to remove any empty positions at the output.
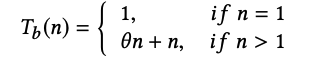
General Case
Where σ - collision rate per iteration, θ - the number of operations required for the
data points to pass through the neural network, e - number of data points that were misordered in the
i-th iteration.
The whole sorting process can be divided into 2 parts:
- Generating several roughly ordered arrays and one ordered conflicting array
- Merging all the roughly ordered arrays
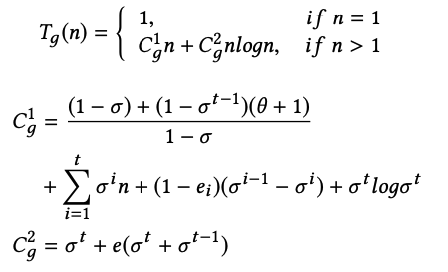
Worst Case
The sorting process is then divided into 3 parts:
- Feeding data elements into the model for ε times
- Sorting all the conflicting data points
- Correcting the out-of-order data elements and merging all the sorted arrays
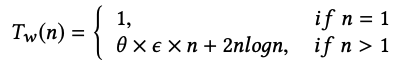
Evaluation
